|
Here I want to
present a way of modelling the Heavens so you can grasp how the stars
move. To understand the motions of the stars, we first have
to have a basic understanding of the earth as a sphere, and of the
Heavens
modelled as a second sphere. For a very simple way of grasping this,
imagine
the earth as a ball inside another, much larger ball. That larger ball
represents the sphere on which the stars seem to be placed. If we
imagine that second ball as spinning once a day, from East to West, clockwise when
facing North, we can
imagine the rotation of the stars.
Now, all of the stars aren't truly placed onto one sphere that is X
miles away; some stars are relatively close, and some are far away, but
to our
eyes, they seem to be on a single sphere, and this gives us a way of
modelling the stars' movements: imagine you are a small point
on that earth ball, inside the larger, spinning ball on which all the
visible stars are painted. Because both the earth and celestial spheres
are round, you can only see
about half of the star ball at any given location at any given time
(neverminding the effect of the Sun's light on the stars' visibility,
of course. You won't be seeing them during the daytime unless there's
an eclipse.).
So, if you were to cut the star ball in half, you'd have a map of the
stars you can see at a given latitude (depending on the time of the
year, i.e., the
position of the Sun).
If you have a half of a ball like that, you can imagine it, if a handle
were added, as a very deep, bell-shaped umbrella, and that, to me, is
the easiest way to picture all this. Simply  imagine an umbrella on which
the stars of the Northern half of the celestial sphere have been
painted on its underside. Now, hold it out in front of you, its handle
parallel to
the floor and pointing North, and then tilt it up toward you according
to
your latitude -- i.e., if you are at 40o latitude North,
tilt the umbrella up 40o relative to the floor. imagine an umbrella on which
the stars of the Northern half of the celestial sphere have been
painted on its underside. Now, hold it out in front of you, its handle
parallel to
the floor and pointing North, and then tilt it up toward you according
to
your latitude -- i.e., if you are at 40o latitude North,
tilt the umbrella up 40o relative to the floor.
Now take the umbrella and hold it over the edge of a round table,
keeping it tilted it toward the North at an angle that matches your
latitude. The table represents the ground you are standing on, the edge
of the table represents the horizon, and as you spin the umbrella, on
its axis, once
each day to mimic the spin of the celestial sphere, stars will
go in and out of sight as they sink below and rise above the horizon.
These stars are always out there, always circling, even during the day
time when the Sun's light prevents our seeing them.
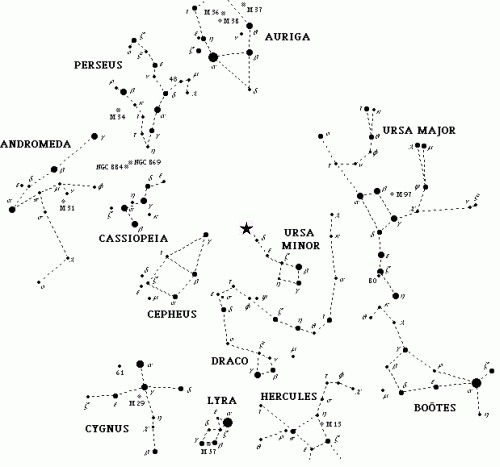
Using the Northernmost Stars as an Example of How
to Form a Mental Image of the Celestial Sphere
Ursa Minor: At the very tip of the
umbrella will be the North Star -- Polaris, a star in a constellation
known as Ursa Minor, or "Little Bear." This constellation has a group
of stars -- an "asterism," or an easily recognizable pattern of stars
that isn't regarded as an official constellation in itself -- that is
known as "The Little Dipper," and Polaris is the very tip of the Little
Dipper's handle.
If you are standing at the North Pole (at 90o N), Polaris
will be directly overhead, so you'd keep the umbrella upright, at a 90o
angle from the floor, for your map of the heavens; the stars above your
head will appear to move in lovely circles with your position at the
center.
If you are around the equator, at 0o latitude, Polaris will
seem to be lying directly on the ground in the distance, and the stars
that form the cup of the Little Dipper will be quickly going in and out
of sight, over and underneath the horizon, circling around it at due
North
(you'd have your umbrella lying so that its handle is flat against the
table).
If you are at around 40o latitude (like Indianapolis and
Naples) and tilt the umbrella properly, Polaris will appear to be 40o
up over the table-horizon. The measure of the altitude over the horizon
of this "Pole
Star" will always equal the latitude of the person doing the measuring.
It is by knowing this that ancient navigators could always find true
North.
Polaris, by the way, is 430 light years away (a "light year" is the distance
light travels in one year) -- that is, when we see the star, we are
seeing it as it appeared 430 years ago (see this beautiful time lapse photograph that shows the
movement of the stars around Polaris, which seems to sit always still
over the tip of our globe).
OK, so now that you have a way of envisioning how the stars move, let's
begin...
|
|
![]()